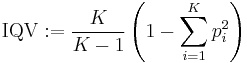Qualitative variation
An index of qualitative variation (IQV) is a measure of statistical dispersion in nominal distributions. There are a variety of these, but they have been relatively little-studied in the statistics literature. The simplest is the variation ratio, while the most sophisticated is the information entropy.
Contents |
Properties
There are various indices of qualitative variation; a number are summarized and devised by Wilcox (Wilcox 1967), (Wilcox 1973), who requires the following standardization properties to be satisfied:
- Variation varies between 0 and 1.
- Variation is 0 if and only if all cases belong to a single category.
- Variation is 1 if and only if cases are evenly divided across all category.[1]
In particular, the value of these standardized indices does not depend on the number of categories or number of samples.
For any index, the closer to uniform the distribution, the larger the variance, and the larger the differences in frequencies across categories, the smaller the variance.
Indices of qualitative variation are in this sense complementary to information entropy, which is maximized when all cases belong to a single category and minimized in a uniform distribution, but they are not complementary in the sense of a particular IQV equaling 1 minus entropy. Indeed, information entropy can be used as an index of qualitative variation.
One characterization of a particular index of qualitative variation (IQV) is as a ratio of observed differences to maximum differences.
Formulae
Wilcox gives a number of formulae for various indices of QV (Wilcox 1973), the first, which he designates DM for "Deviation from the Mode", is a standardized form of the variation ratio, and is analogous to variance as deviation from the mean.
One formula for IQV,[2] given as M2 in (Gibbs 1975, p. 472) is:
where K is the number of categories, and 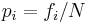 is the proportion of observations that fall in a given category i. The factor of
is the proportion of observations that fall in a given category i. The factor of 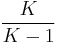 is for standardization.
is for standardization.
The unstandardized index, 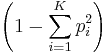 , denoted as M1 (Gibbs 1975, p. 471), can be interpreted as the likelihood that a random pair of samples will belong to the same category (Lieberson 1969, p. 851), so this formula for IQV is a standardized likelihood of a random pair falling in the same category. M1 and M2 can be interpreted in terms of variance of a multinomial distribution (Swanson 1976) (there called an "expanded binomial model").
, denoted as M1 (Gibbs 1975, p. 471), can be interpreted as the likelihood that a random pair of samples will belong to the same category (Lieberson 1969, p. 851), so this formula for IQV is a standardized likelihood of a random pair falling in the same category. M1 and M2 can be interpreted in terms of variance of a multinomial distribution (Swanson 1976) (there called an "expanded binomial model").
Evaluation of indices
Different indices give different values of variation, and may be used for different purposes: several are used and critiqued in the sociology literature especially.
If one wishes to simply make ordinal comparisons between samples (is one sample more or less varied than another), the choice of IQV is relatively less important, as they will often give the same ordering.
In some cases it is useful to not standardize an index to run from 0 to 1, regardless of number of categories or samples (Wilcox 1973, pp. 338), but one generally so standardizes it.
See also
Notes
- ^ This can only happen if the number of cases is a multiple of the number of categories.
- ^ IQV at xycoon
References
- Gibbs, Jack P.; Poston, Jr., Dudley L. (March 1975), "The Division of Labor: Conceptualization and Related Measures", Social Forces 53 (3): 468–476, doi:10.2307/2576589, JSTOR 2576589
- Lieberson, Stanley (December 1969), "Measuring Population Diversity", American Sociological Review 34 (6): 850–862, doi:10.2307/2095977, JSTOR 2095977
- Swanson, David A. (September 1976), "A Sampling Distribution and Significance Test for Differences in Qualitative Variation", Social Forces 55 (1): 182–184, doi:10.2307/2577102, JSTOR 2577102
- Wilcox, Allen R. (1967), Indices of qualitative variation, http://www.ornl.gov/info/reports/1967/3445605133753.pdf
- Wilcox, Allen R. (June 1973), "Indices of Qualitative Variation and Political Measurement", The Western Political Quarterly 26 (2): 325–343, doi:10.2307/446831, JSTOR 446831